شبکه‌های بلوری چیست و چطور تشکیل می شود

۱- مقدمه

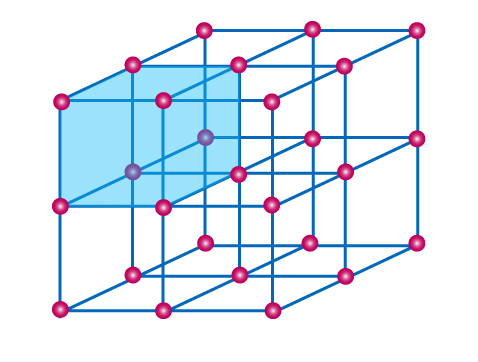
پس از آشنایی با مفاهیم اولیه بلورشناسی باید بدانید که مطالعات بلورشناسی (مدل‌سازی‌های ریاضی و بررسی‌های آزمایشگاهی) نشان داده است که سیستم‌های بلوری مختلفی را در دو و سه‌بعد می‌توان تعریف و بررسی نمود. اساس این بررسی‌ها وجود تقارن در این ساختارها و نوع آن تقارن‌هاست. در این مقاله هدف بررسی این تقارن‌ها نیست و صرفا سعی می‌شود نتیجه آنها که همان سیستم‌های بلوری در دو و سه‌بعد هستند، توضیح داده شود. البته نقص های بلوری در این ساختارها وجود دارد که در مقالات بعدی به آن پرداخته شده است.

۲- سیستم‌های بلوری

 اتم‌ها در ساختارهای بلوری به حالت‌های مختلفی در کنار هم قرار می‌گیرند، قرارگیری اتم‌ها در این ساختارهای بلوری نقش مهمی در تعیین ویژگی‌ها و خواص مواد دارد. سیستم‌های بلوری را می‌توان به دو دسته کلی سیستم‌های بلوری دوبعدی و سه‌بعدی طبقه‌بندی کرد. برای شناخت بیشتر این سیستم‌ها، در این بخش سیستم‌های بلوری دوبعدی و سه‌بعدی که اتم‌ها در یک ساختار منظم می‌توانند در کنار یکدیگر قرار بگیرند معرفی شده و بررسی خواهد شد.

۱-۲- سیستم‌های بلوری در دوبعد

ساده‌ترین شکلی که با آن می‌توان یک صفحه را پر نمود متوازی‌الاضلاع است. برای مشخص نمودن مشخصات یک متوازی‌الاضلاع نیز کافی است دو بردار ضلع آن و زاویه بین آنها را تعیین نمود (شکل1).

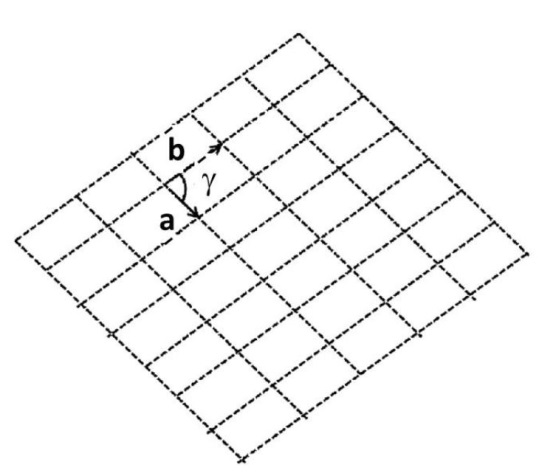
شکل۱- مشخص نمودن یک سیستم دوبعدی با دو بردار و زاویه بین آنها

این دو بردار و زاویه بین‌شان می‌توانند مقادیر مختلفی داشته باشند، حالت‌های مختلف این سه متغیر ( دو بردار و زاویه بین آنها) به چهار سیستم دوبعدی می‌انجامد،که در شکل۲ نشان داده شده است [۱]. این چهار سیستم شامل، سیستم مورب، مستطیلی، شش ضلعی و مربعی است.

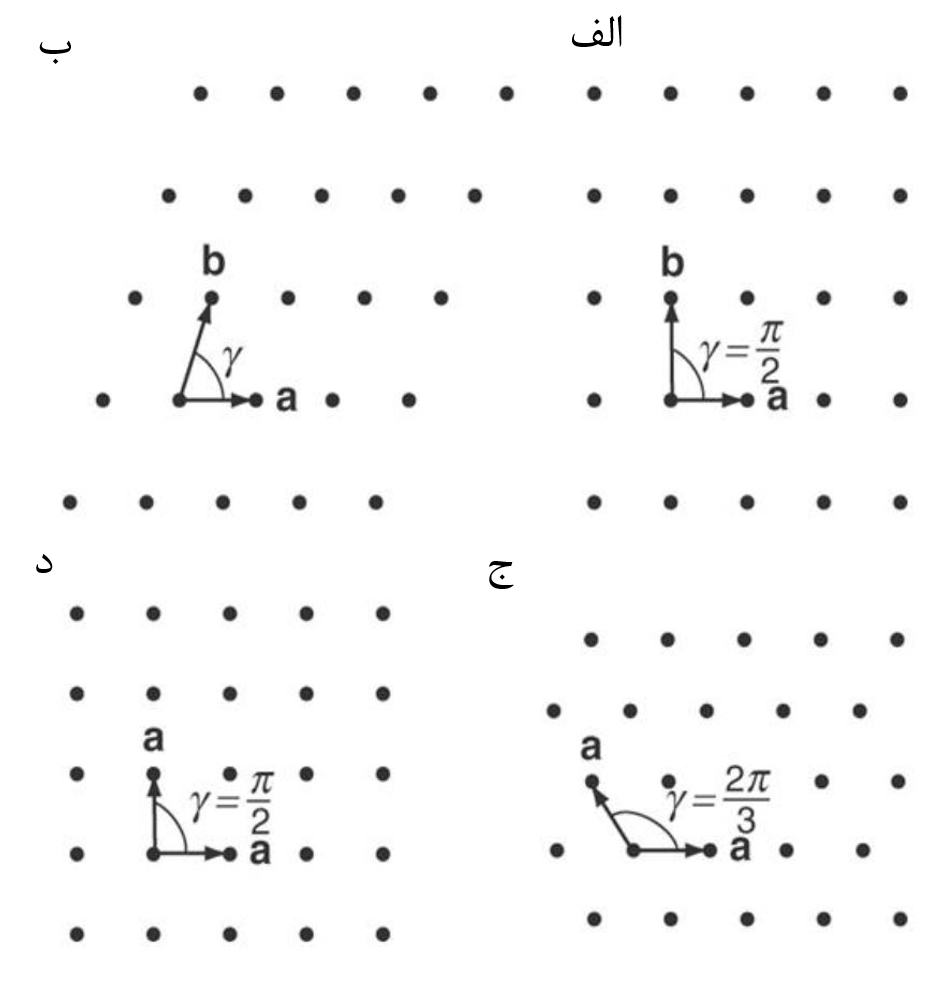
شکل۲- چهار سیستم بلوری مختلف در دوبعد (الف) سیستم مستطیلی(ب) مورب^[۱] (ج) شش‌ضلعی (د) مربعی[۱]

همان‌طور که در شکل ۲ مشاهده می‌شود، در سیستم مورب ارتباط خاصی بین اضلاع و زاویه بین آنها وجود ندارد؛ در سیستم مستطیلی زاویه بین دو بردار ۹۰‌درجه است؛ در سیستم شش‌ضلعی دو بردار با یکدیگر برابرند و زاویه بین آنها نیز ۱۲۰‌درجه است و در سیستم مربعی زاویه بین دو بردار ۹۰‌درجه و اندازه دو بردار نیز با یکدیگر برابر است.

همان‌طور که در مقاله مفاهیم اولیه بلورشناسی گفته شد، در این سیستم‌ها می‌توان یک سلول واحد با شرایط گفته شده را تعریف نمود و از آن به عنوان نماینده هر یک از این سیستم‌های بلوری در دوبعد نام برد و با تکرار آنها در دوبعد به این سیستم‌های بلوری رسید.

یکی از نانوساختارهای معروفی که ساختار دوبعدی دارد گرافن است. گرافن ساختاری لانه زنبوری از اتم‌های کربن است، که فاصله بین هر دو اتم در آن حدود ۰/۱۴۲ نانومتر می‌باشد. در شکل۳ ساختار دوبعدی گرافن نمایش داده شده است. همان‌گونه که درشکل‌های ۲ و ۳ مشاهده می‌شود، ساختار بلوری گرافن مطابق سیستم شش‌ضلعی می‌باشد. البته این توضیحات در حالت ایده‌آل که ناخالصی و نقصی وجود نداشته باشد صدق می‌کند.

شکل ۳- ساختار دوبعدی گرافن

۲-۲- سیستم‌های بلوری در سه‌بعد

در شکل۴ چهارده شبکه براوه نمایش داده شده است.

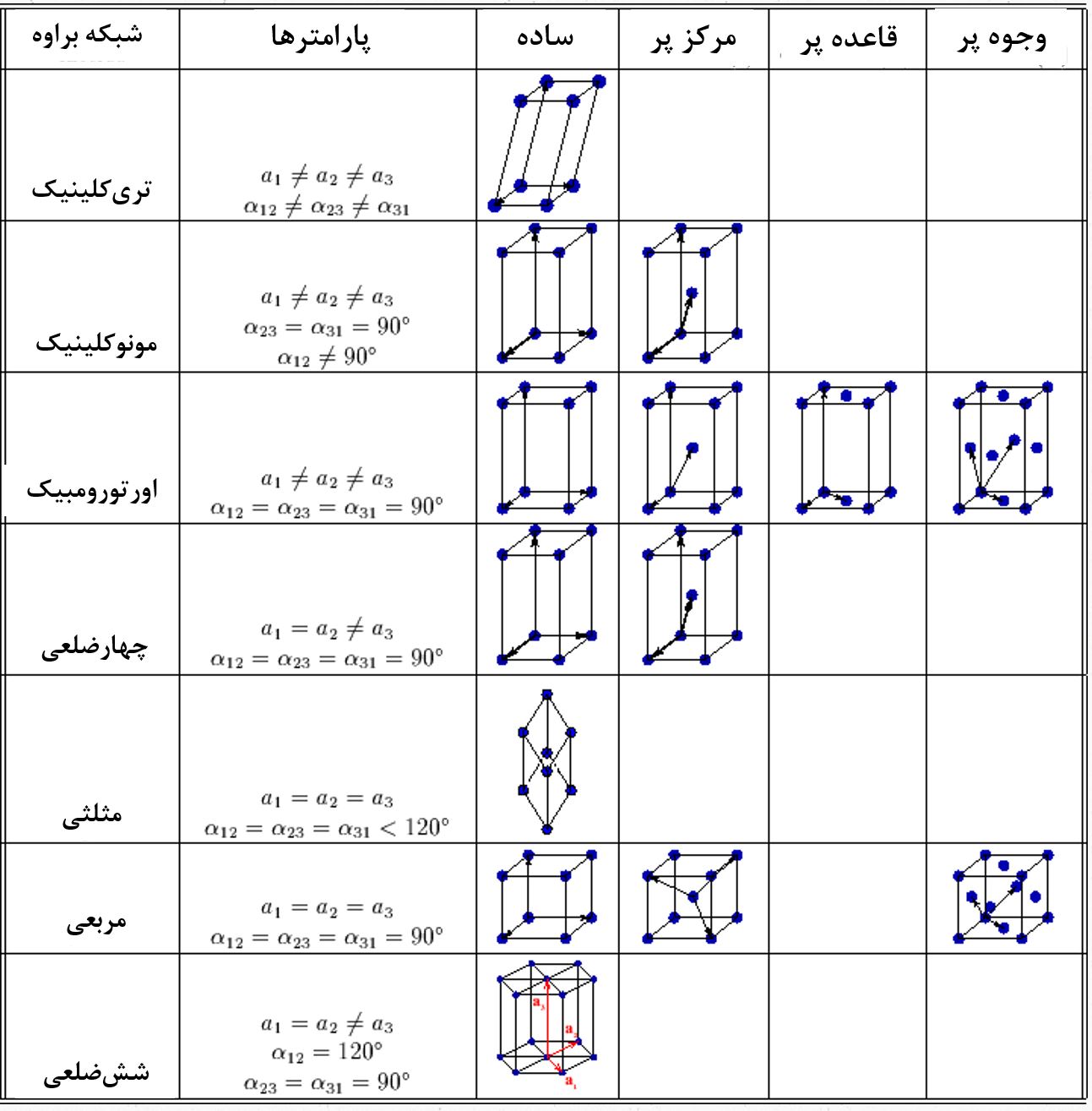
شکل۴- چهارده شبکه براوه [۱]. در بخش پارامترهای نمایش داده شده در شکل، پارامترهای a₁, a₂,a₃ همان a, b, c و α₁₂ , α₂₃ , α₁₃ همان α, β, γ که در مقاله بیان شد، می‌باشند و صرفا از نماد متفاوتی برای نشان دادن آن‌ها استفاده شده است.

چهارده شبکه طبق مدل‌سازی‌های ریاضی و همین‌طور بررسی‌های آزمایشگاهی مشخص شده‌اند و هیچ کدام از آنها با یکدیگر یکسان نیستند. همچنین ساختار دیگری نیست که شرایط لازم را دارا باشد و مشابه این 14 شبکه نباشد؛ برای مثال اگر گفته شود چرا چهارضلعی قاعده پر در این لیست حضور ندارد، دلیلش این است که اگر از جهت دیگری به آن نگاه شود، چهارضلعی قاعده پر دقیقا مشابه چهارضلعی ساده است [۲].

مطابق شکل۴، چهارده شبکه براوه از ۷ شبکه اصلی و ۷ شبکه فرعی تشکیل شده‌اند. ۷ شبکه اصلی شامل شبکه‌های مکعبی ساده، تتراهدرال (چهارضلعی)، اورتورومبیک، رمبوهدرال (مثلثی)، هگزاگونال (شش‌ضلعی)، مونوکلینیک و تری‌کلینیک هستند. ۷ شبکه فرعی با توجه به مرکز پر بودن، قاعده پر بودن و یا وجوه پر بودن از ۷ شبکه اصلی تشکیل می‌شوند. برای مشخص نمودن هر یک این ۱۴ شبکه براوه لازم است تا سه بردار تشکیل‌دهنده سلول واحد و همین‌طور زوایای بین آنها (مجموعا سه زاویه) را بیان نمود. در شکل‌۴ برای هرکدام از ۷ ساختار پایه، این زوایا و بردارها بیان شده‌اند [۲].

همان‌طور که گفته شد در این ۱۴ شبکه براوه فرض بر یکسان بودن موتیف‌ها است. یعنی این شبکه‌ها صرفا برای مواد بلوری با یک نوع اتم به‌کار می‌روند. برای مواد بلوری با دو یا چند نوع اتم (مثل سرامیک‌ها) شبکه‌های غیربراوه‌ای وجود دارند که از تلفیقی از چند شبکه براوه حاصل شده‌اند. برای اطلاعات بیشتر در این رابطه می‌توانید به مقاله " نانومواد سرامیکی" مراجعه کنید. در اینجا صرفا به نمایش ساختارهای کریستالی معروف سرامیک‌ها بسنده می‌شود (شکل۵). بسیاری از مواد سرامیکی دیگر نیز ساختار بلوری مشابه دارند و مشابه همین ساختارها نام‌گذاری می‌شود.

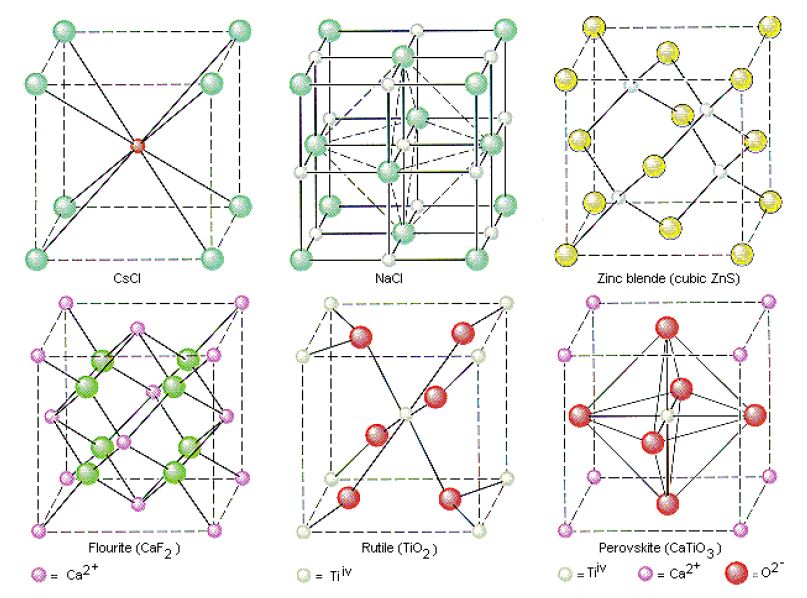
شکل۵- ساختارهای کریستالی معروف سرامیک‌ها (شبکه‌های غیر براوه) [۳]

از بین شبکه‌های براوه نامبرده شده در بالا، شبکه‌های مکعبی و شش‌ضلعی اهمیت بیشتری دارند، چرا که بیشتر مواد متداول بلوری ساختار مکعبی یا شش‌ضلعی دارند. به همین دلیل در ادامه به بررسی بیشتر این شبکه‌ها می‌پردازیم.

۱-۲-۲- شبکه‌های مکعبی

همانطور که در بالا بیان شد شبکه‌های مکعبی به سه گروه مکعبی ساده (SC)^[۲]، مکعبی مرکز پر(BCC) ^[۳] و مکعبی وجوه پر (FCC)^[۴] تقسیم می‌شوند (بیان این شبکه‌ها با حروف اختصاری گفته شده، مرسوم است و به همین دلیل آنها را نیز به خاطر بسپارید). در شکل۶ این سه شبکه آورده شده است.

همانطور که در شکل۶ مشاهده می‌شود، در مکعب مرکز پر یک اتم در وسط مکعب قرار گرفته است و هشت اتم هم در رئوس مکعب؛ در مکعبی وجوه پر ۶ اتم در وجوع مکعب و ۸ اتم هم در رئوس مکعب قرار گرفته‌اند. به‌صورت مرسوم برای نمایش این شبکه‌های مکعبی ردیف اول شکل ۶ نمایش داده می‌شود، که علت آن فهم راحت‌تر و نمایش ساده‌تر آن است، ولی باید دقت نمود که در واقعیت این شبکه‌ها به شکل ردیف دوم شکل۶ هستند. ردیف سوم شکل ۶ نیز کمک می‌کند تا تعداد اتم‌های خالص هرکدام از شبکه‌ها را محاسبه نمود، که در ادامه به آن می‌پردازیم [۳].

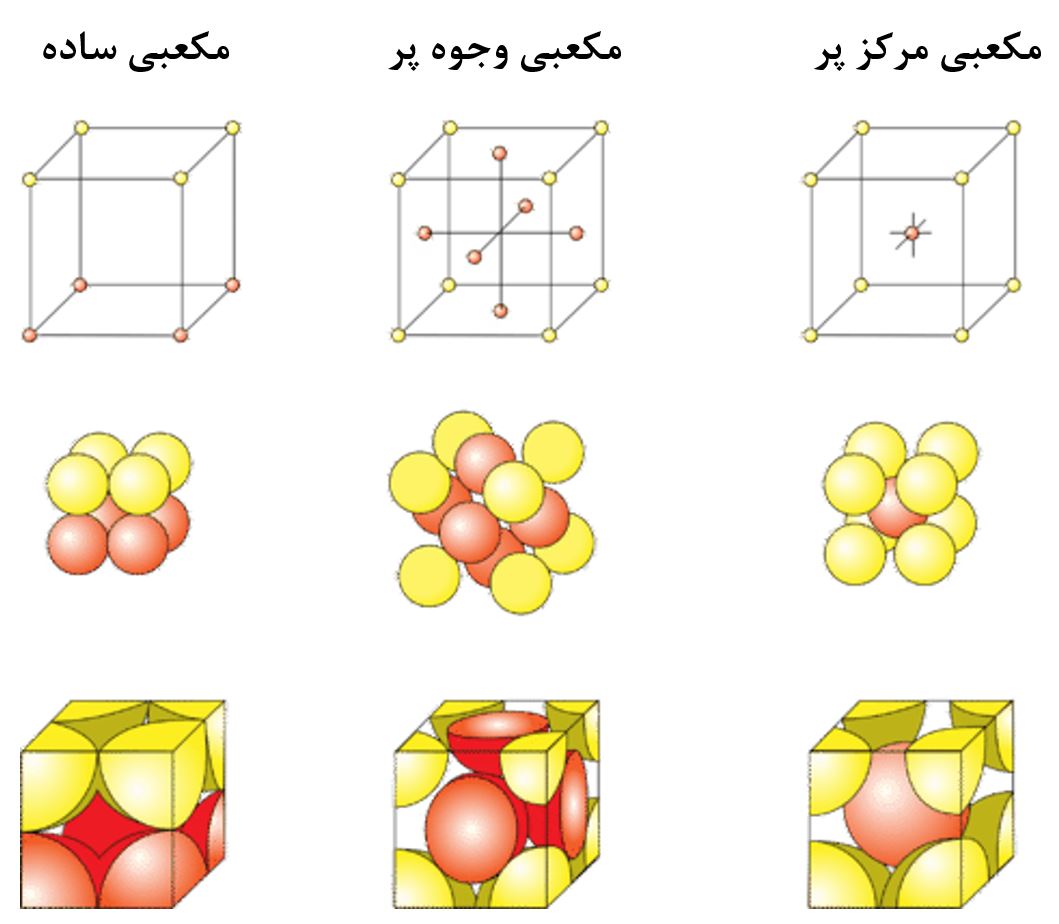
شکل۶- شماتیک سه شبکه مکعبی ساده، مرکز پر و وجوه پر[۳]

۱-۱-۲-۲- شبکه مکعبی ساده

برای بررسی این شبکه‌ها چندین عامل مهم است. این عوامل عبارتند از تعداد اتم‌های خالص در یک سلول واحد، جهت فشرده^[۵]، فاکتور فشردگی اتمی (APF)^[۶] و عدد همسایگی.

برای مشخص نمودن تعداد اتم‌های خالص سلول واحد یک شبکه مکعبی ساده، به ردیف سوم شکل ۵ نگاه کنید. همان‌طور که در شکل مشاهده می‌شود سلول واحد این شبکه از هشت اتم موجود در رئوس مکعب حاصل شده است. هم‌چنین تنها یک هشتم آن اتم به صورت خالص متعلق به آن سلول واحد است (یک اتم به صورت هم‌زمان در هشت سلول واحد مکعبی وجود دارد پس یک هشتم آن متعلق به یک سلول واحد است). در نتیجه تعداد اتم‌های خالص در سلول واحد شبکه مکعبی ساده برابر است با:        $8\times \frac{1}{8}=1$

پارامتر شبکه در شبکه‌های کریستالی به نزدیک‌ترین فاصله بین اتم‌ها در شبکه کریستالی گفته می‌شود. جهت فشرده در این شبکه به جهتی گفته می‌شود که اتم‌ها با یکدیگر مماس باشند. در واقع همواره مقدار پارامتر شبکه برابر فاصله بین دو اتم در جهت فشرده است. در راستای جهت فشرده هیچ فاصله‌ای بین اتم‌ها وجود ندارد. جهت فشرده در هر یک از ساختارهای مکعبی با دیگری متفاوت است و بستگی به نحوه چینش اتم‌ها در کنار یکدیگر دارد. همانطور که در شکل ۷-الف مشاهده می‌شود جهت فشرده در شبکه مکعبی ساده در راستای اضلاع مکعب است. مشخص نمودن جهت فشرده برای محاسباتی که در ادامه آورده شده‌اند بسیار مهم است.

عدد همسایگی نیز مطابق شکل۷-ب به تعداد اتم‌هایی که در همسایگی هریک از اتم‌ها در شبکه باشد گفته می‌شود. تشخیص عدد همسایگی در بعضی از ساختارهای بلوری به علت پیچیدگی‌های ساختار، دشوار است. عدد همسایگی برای شبکه مکعبی ساده برابر با ۶ است (۲ اتم همسایه در هر سه راستای محور x، y و z ).

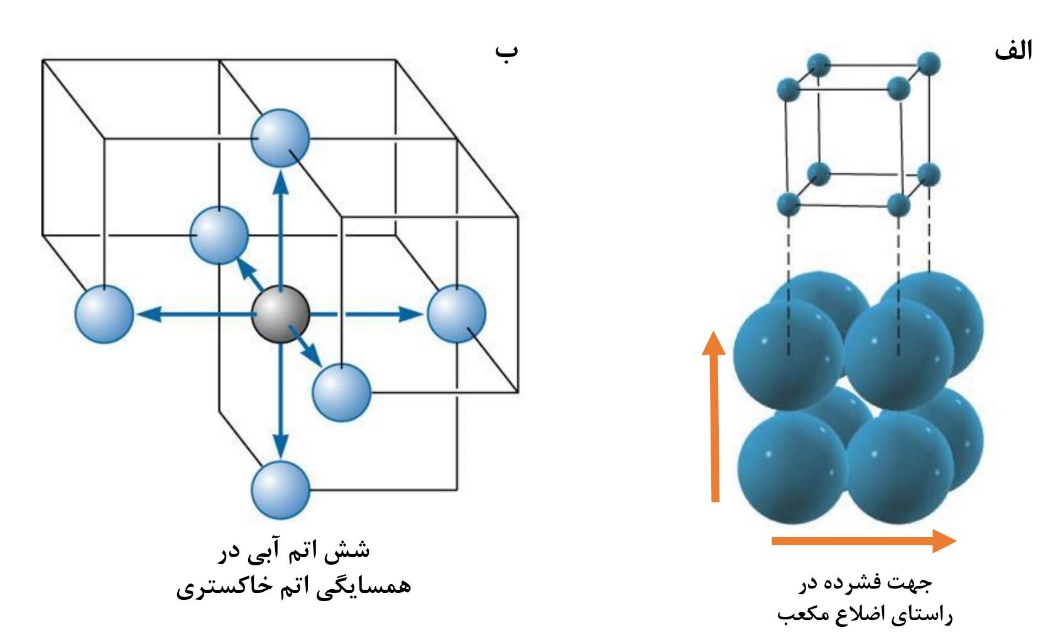
شکل۷- نمایش الف) جهت فشرده و ب) عدد همسایگی در شبکه مکعبی ساده

یکی دیگر از مشخصه‌های بلور که اهمیت فراوانی دارد، فاکتور فشردگی اتمی است. فاکتور فشردگی اتمی نشان‌دهنده این است که چقدر از حجم یک سلول واحد توسط اتم‌ها اشغال شده است و هرچه بیشتر باشد نشان‌دهنده فشردگی بیشتر اتم‌ها در آن سلول واحد است. محاسبه فاکتور فشردگی در معادله1 آورده شده است:

$\mathrm{اتمی} \mathrm{فشردگی} \mathrm{فاکتور} =\frac{\mathrm{تعداد} \mathrm{اتم} \mathrm{های} \mathrm{موجود} \mathrm{در} \mathrm{سلول} \mathrm{واحد} \times \mathrm{حجم} \mathrm{تک} \mathrm{اتم}}{\mathrm{حجم} \mathrm{سلول} \mathrm{واحد}} \left(\mathrm{۱}\right)$

همان‌طور که گفته شد در شبکه مکعبی ساده هر سلول واحد شامل ۱ اتم است؛ هم‌چنین برای محاسبه حجم اتم‌ها، آنها را کره فرض می‌کنیم؛ در این صورت حجم یک اتم برابر است با:$\frac{4}{3}\pi R^3$
 حجم سلول واحد نیز برابر است با مکعب طول هر ضلع آن، یعنی: $a^3$.

هم‌چنین باتوجه به تعیین جهت فشرده دانستیم که در شبکه کریستالی مکعبی ساده پارامتر شبکه دو برابر شعاع اتم هاست: (a=2R)

 درنتیجه داریم:

$\frac{1\times {\displaystyle \frac{4}{3}}\pi R^3}{{\left(2R\right)}^3}=\frac{{\displaystyle \frac{4}{3}}\pi R^3}{8R^3}=\frac{\pi }{6}=0.524=52.4\% \left(\mathrm{۲}\right)$  

بنابراین، فاکتور فشردگی اتمی در شبکه مکعبی ساده برابر با ۵۲% می‌باشد.

۲-۱-۲-۲-  شبکه مکعبی مرکز پر (BCC)

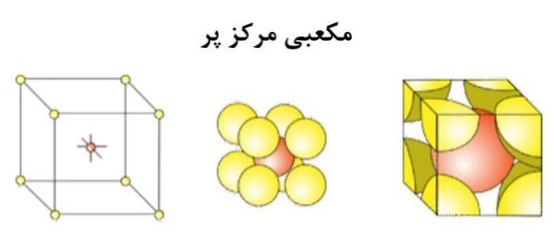
شکل۸- تصویر طرحی از شبکه مکعبی مرکز پر

مشابه شبکه مکعبی ساده، برای شبکه مکعبی مرکز پر نیز عدد همسایگی، جهت فشرده و فاکتور فشردگی اتمی را محاسبه خواهیم کرد. مطابق ردیف سوم شکل۸، مشاهده می‌شود که در سلول واحد این شبکه یک اتم به صورت کامل در وسط قرار دارد و هشت اتم نیز که هرکدام یک هشتم‌شان متعلق به آن سلول واحد است در آن وجود دارند، در نتیجه تعداد اتم‌های خالص در سلول واحد این شبکه برابراست با:

$1+(8\times \frac{\mathrm{۱}}{8})=\mathrm{۲} \left(\mathrm{۳}\right)$

عدد همسایگی در این ساختار برابر است با ۸. برای درک بهتر این امر می‌توانید اتمی که در مرکز این ساختار قرار گرفته است را در نظر بگیرید که هشت اتم در همسایگی آن قرار گرفته‌اند.

جهت فشرده در این شبکه عبارت است از قطر مکعب. برای فهم بهتر آن به شکل ۹ نگاه کنید.

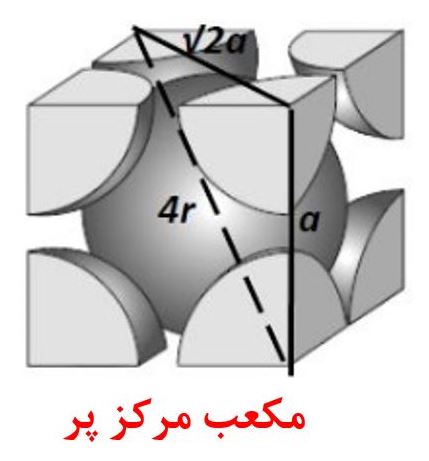
شکل۹- نمایش جهات فشرده و رابطه بین اندازه ضلع مکعبی و شعاع اتم‌ها در شبکه مکعبی مرکز پر[۳]

مطابق شکل۹، در شبکه مکعبی مرکز پر رابطه بین پارامتر شبله و شعاع اتم‌ها در راستای قطر مکعب داریم:

$\sqrt{3} a=4R\to a=\frac{4R}{\sqrt{3}} \left(\mathrm{۴}\right)$

از این رو می‌توان فاکتور فشردگی اتمی در این شبکه را محاسبه نمود:

$\frac{2\times {\displaystyle \frac{4}{3}}\pi R^3}{a^3}=\frac{{\displaystyle \frac{8}{3}}\pi R^3}{{\left(\frac{4R}{\sqrt{3}}\right)}^3}=\frac{{\displaystyle \frac{8}{3\pi }}}{\frac{64}{3\sqrt{3}}}=\frac{\sqrt{3}\pi }{8}=0.68=68\% \left(\mathrm{۵}\right)$

۳-۱-۲-۲- شبکه مکعبی وجوه پر (FCC)

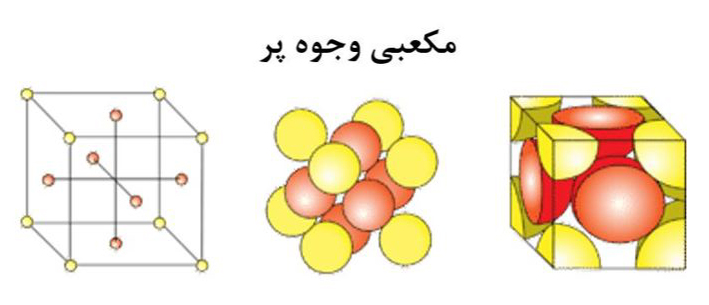
شکل۱۰- تصویر طرحی از شبکه مکعبی وجوه پر

مطابق شکل۱۰، در سلول واحد شبکه مکعبی وجوه پر، ۶ اتم در وجوه قرار دارند که نصفی از آنها به صورت خالص مربوط به سلول واحد هستند و هشت اتم که یک هشتم‌شان متعلق به سلول واحد است در رئوس مکعب قرار دارند، بنابراین برای محاسبه تعداد اتم خالص سلول واحد در این شبکه داریم:

$(6\times \frac{1}{2})+(8\times \frac{ 1}{8})=4 \left(\mathrm{۶}\right)$

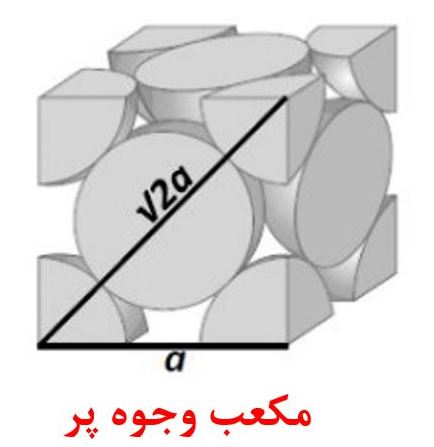
شکل۱۱- نمایش جهات فشرده و رابطه بین اندازه ضلع مکعبی و شعاع اتم‌ها در شبکه مکعبی وجوه پر [۳]

عدد همسایگی نیز در این ساختار برابر است با ۱۲. همچنین برای تعیین جهت فشرده باید به شکل۱۱ توجه نمود. مطابق این شکل دیده می‌شود که قطر وجوه (برابر با اندازه ضلع ضربدر رادیکال۲) جهت فشرده در این ساختار است؛ همچنین رابطه بین اندازه ضلع و شعاع اتم‌ها در این ساختار عبارت است از:

$a\sqrt{2}=4R\to a=\frac{4R}{\sqrt{2}} \left(\mathrm{۷}\right)$

مطابق توضیحات قبلی، محاسبه فاکتور فشردگی اتمی نیز به این صورت انجام می‌شود:

$\frac{4\times {\displaystyle \frac{4}{3}}\pi R^3}{a^3}=\frac{{\displaystyle \frac{16}{3}}\pi R^3}{({\displaystyle \frac{4R}{\sqrt{2}}}{)}^3}=\frac{{\displaystyle \frac{16}{3}}\pi }{{\displaystyle \frac{64}{2\sqrt{2}}}}=\frac{\sqrt{2}\pi }{6}=0.74=74\% \left(\mathrm{۸}\right)$

همان‌طور که در این محاسبات مشاهده شد شبکه FCC بیشترین و شبکه SC کمترین فاکتور فشردگی اتمی را در بین شبکه‌های مکعبی دارا می‌باشند.

۲-۲-۲- شبکه شش‌ضلعی فشرده(HCP) ^[۷]

شبکه شش‌ضلعی فشرده و نحوه قرارگیری اتم‌ها در این شبکه در شکل ۱۲ نمایش داده شده است.

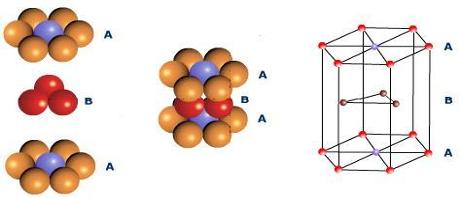
شکل۱۲- نمایش شبکه شش‌ضلعی فشرده

مطابق شکل۱۲، ۳ اتم به‌طور کامل درون سلول واحد وجود دارند؛ دو اتم بر روی قاعده بالا و پایین نصف‌شان متعلق به سلول واحد است و ۱۲ اتم روی رئوس نیز یک ششم‌شان متعلق به سلول واحد است پس داریم:

$3+(2\times \frac{1}{2})+(12\times \frac{ 1}{6})=6 \left(\mathrm{۹}\right)$

عدد همسایگی در این شبکه نیز مشابه مکعب وجوه پر برابر با ۱۲ می‌باشد. جهت فشرده را نیز می‌توان هریک از اضلاع شش‌ضلعی دو قاعده در نظر گرفت (چرا که بر روی این اضلاع اتم‌ها با یکدیگر مماسند) که طبق آن هر ضلع آن برابر با دو شعاع اتمی می‌شود.

فاکتور فشردگی اتمی نیز مشابه شبکه مکعبی وجوه پر برابر با ۷۴% است.

قابل ذکر است که برای این شبکه سلول واحد دیگری نیز می‌توان در نظر گرفت. برای این‌کار سلول واحد نمایش داده شده در شکل۱۲ را می‌توان به سه مستطیل هم اندازه و یکسان تقسیم کرد و آنها را به عنوان سلول واحد در نظر گرفت. در آن صورت تعداد اتم‌های خالص هر سلول واحد برابر ۲ می‌شود. اما فاکتور فشردگی اتمی و عدد همسایگی تغییری نمی‌کند، چرا که مرتبط با کل شبکه است و تعیین سلول‌های واحد مختلف بر روی آن تاثیری ندارد.

تمرین ۱

اگر اندازه هر ضلع شش­‌ضلعی قاعده‌­ها را a و ارتفاع سلول واحد را c بنامیم، برای محاسبه فاکتور فشردگی شبکه HCP داریم:

$\frac{(6\times {\displaystyle \frac{4}{3}}\pi R^3)}{{\displaystyle \frac{3\surd 3}{2}}{a}^{2}c}$

مخرج این عبارت برابر با حجم سلول واحد است. برای محاسبه آن باید ارتباطی بین ارتفاع سلول واحد و اندازه هر ضلع شش‌­ضلعی قاعده‌­ها پیدا نمود. رابطه‌­ای بین آنها پیدا نموده و طبق آن فاکتور فشردگی اتمی شبکه HCP را که در بالا بیان شد را محاسبه نمایید.

تمرین ۲

افزایش حجم ناشی از تبدیل ماده‌ای بلوری  با ساختار شبکه FCC به BCC  برابر با %۸/۱ است. محاسباتی که به این میزان افزایش حجم می‌انجامد را انجام دهید. (راهنمایی: با توجه به تعداد اتم‌های خالص در هریک از این شبکه‌ها، به ازای هر سلول واحد شبکه FCC دو سلول واحد شبکه BCC ایجاد می‌شوند.

۳- جهات و صفحات بلوری

اندیس‌های میلر به منظور تعریف و مشخص نمودن جهات و صفحات بلوری به کار می‌روند. در ادامه به معرفی این اندیس‌ها پرداخته می‌شود. با توجه به اهمیت بیشتر شبکه‌های بلوری مکعبی نسبت به سایر شبکه‌های براوه، در این بخش به روش تعیین جهات و صفحات بلوری در شبکه‌های مکعبی اشاره خواهد شد و در این بررسی‌ها ابتدا یک دستگاه مختصات مناسب و راست‌گرد انتخاب شده است.

۱-۳- جهت‌های میلر

برای مشخص نمودن جهات میلر کافی است تا مختصات نقطه انتهایی در شبکه را از مختصات نقطه ابتدایی در شبکه کم نمود؛ سپس در صورتی‌ که عدد حاصل صحیح نبود آن را در کوچکترین مضرب ممکن جهت صحیح شدن تمام مولفه‌های اندیس جهات ضرب نمود. هم‌چنین در بیان اندیس‌های میلر علامت منفی گذاشته نمی‌شود و به جای آن علامت بار (خط تیره بالای عدد) گذاشته می‌شود. برای فهم بهتر این توضیحات به شکل۱۳ توجه کنید.

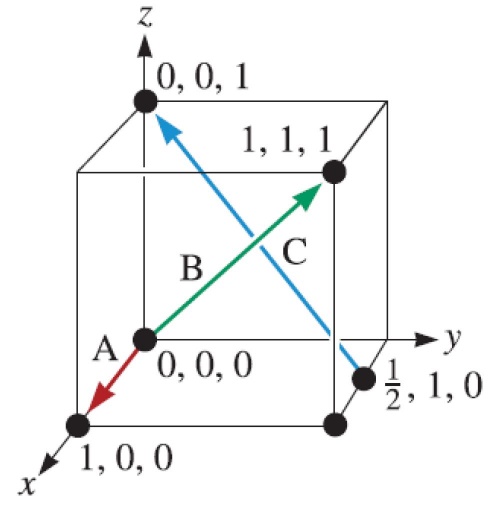
شکل۱۳- نمایش تعدادی جهت میلر در شبکه مکعبی [۲]

برای مثال در شکل۱۳ فلش سبز رنگ جهت [۱ ۱ ۱] را نمایش می‌دهد چون این بردار در هر سه جهت x، y و z یک واحد نسبت به نقطه مبدا جلو رفته است. اما فلش آبی رنگ در جهت x نیم واحد عقب رفته است، در جهت y یک واحد عقب رفته است و در جهت z یک واحد جلو رفته است. یعنی می‌توانیم بنویسیم ۱+ , ۱- , ۰/۵- . حال برای صحیح شدن تمام این مولفه‌ها آنها را در ۲ ضرب می‌کنیم و همین‌طور به جای علامت منفی از علامت بار استفاده می‌کنیم؛ در نتیجه اندیس میلر فلش آبی جهت [ ۲] را نشان می‌دهد. فلش قرمز رنگ نیز جهت [۱۰۰] را نشان می‌دهد چرا که تنها در راستای x حرکت کرده است.

همان‌طور که در بالا دیدید جهات در درون براکت آورده می‌شوند. هم‌چنین خانواده جهات را با <> نشان می‌دهند. برای مثال در شبکه‌های مکعبی خانواده <۱۰۰> شامل تمام جهت‌های $\left[100\right] \left[010\right] \left[001\right] [\overline{1} 00] [0\overline{1} 0] [00\overline{1} ]$ می‌باشد. دلیل بیان خانواده جهات این است که در بسیاری از موارد خواص مختلف در خانواده جهات یکسان است. هم‌چنین بر روی خانواده جهات مشخصه مهمی همچون فاکتور فشردگی خطی (طول اتم‌های موجود در آن جهت تقسیم بر طول جهت) یکسان است [۲].

تمرین۳

حال با یاد گرفتن اندیس میلر جهات بلوری، جهات فشرده در شبکه‌های SC ، BCC و FCC را تعیین کنید.

۲-۳- صفحات میلر

منظور از صفحه، تمام صفحات موازی با هم در بلور هستند که با یکدیگر فواصل برابری دارند. هر دسته صفحه در یک بلور، اندیس میلر خاص خود را دارا می‌باشند. تعدادی از صفحات میلر و اندیس آنها در شکل ۱۴ آورده شده است.

هم‌چنین علامت صفحات میلر () و علامت خانواده صفحات میلر {} است.

برای این منظور باید ابتدا نقاط برخورد این صفحات را با سه محور مشخص کرد، سپس آنها را معکوس نمود و با کمترین نسبت ممکن آنها را نوشت. برای مثال برای صفحه (۱۰۰) این‌گونه اندیس میلر صفحه را مشخص می‌کنیم:

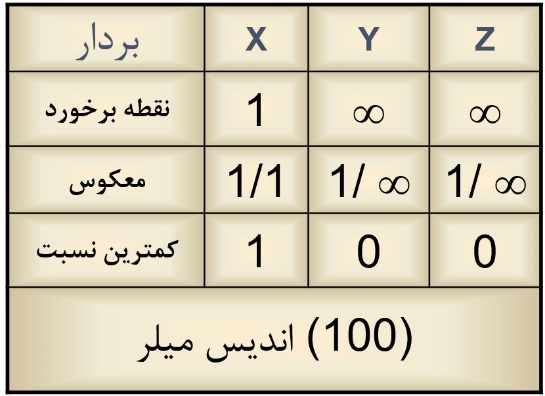
دقت کنید که منظور از بی‌نهایت این است که این صفحه با محورهای y و z موازی است و درنتیجه آنها را در بی‌نهایت قطع می‌کند. هم‌چنین معکوس بی‌نهایت نیز برابر است با صفر. در اینجا نیز به جای منفی از علامت بار استفاده می‌شود.

اگر مشابه جدول بالا برای صفحه (۱۱۱) نقاط تقاطع با سه محور را مشخص کنیم، نقطه برخورد در هر سه محور ۱ خواهد بود. معکوس ۱ نیز برابر با ۱ است. در نتیجه اندیس میلر این صفحه که در شکل ۱۴  نشان داده شده است برابر با (۱۱۱) است.

می‌توانید به‌ عنوان تمرین سه صفحه دیگری که در شکل ۱۴ نشان شده است را خودتان بیابید.

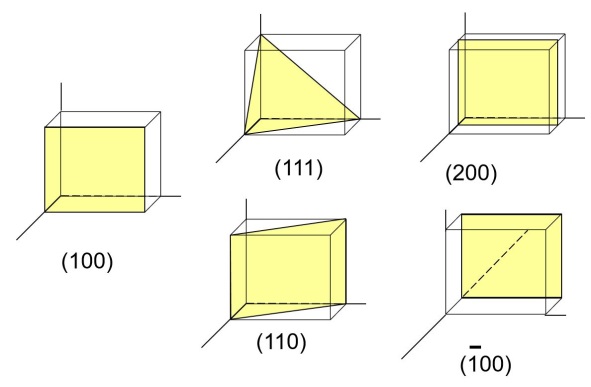
شکل۱۴- تعدادی از صفحات میلر شبکه مکعبی و اندیس صفحه میلر آنها [۲]

همان‌طور که در ابتدا گفته شد در این بررسی‌ها ابتدا مختصات مناسب و راست‌گرد انتخاب می‌شود. اگر صفحه موردنظر از مبدا می‌گذشت کافی است تا مبدا را به یک نقطه مناسب دیگر انتقال بدهید.

۳- جمع‌بندی و نتیجه‌گیری

سیستم‌های بلوری در سه‌بعد به دو دسته شبکه‌های براوه و شبکه‌های غیربراوه تقسیم می‌شوند؛ شبکه‌های براوه دارای اتم‌های یکسان و شبکه‌های غیربراوه دارای دو یا چند نوع اتم (مثل سرامیک‌ها) هستند. شبکه‌های براوه دارای ۱۴ حالت مختلف می‌باشند که از مهم‌ترین آنها می‌توان به شبکه‌های مکعبی SC، BCC و FCC و همین‌طور شبکه شش‌ضلعی فشرده اشاره نمود. بررسی مشخصه‌های این شبکه‌ها همچون تعداد اتم خالص سلول واحد، عدد همسایگی و فاکتور فشردگی اتمی اهمیت فراوانی دارد. با دانستن این متغیرها می‌توان بعضی از مشخصه‌های موادی که این سیستم‌های بلوری را دارا می‌باشند را مشخص نمود. اندیس‌های میلر نیز به منظور تعریف و مشخص نمودن جهات و صفحات بلوری به کار می‌روند. آنالیز پراش اشعه ایکس اطلاعات ارزشمندی از ساختار بلوری مواد بدست می‌دهد که در مقاله آنالیز پراش اشعه ایکس با این روش آشنا خواهید شد.

برای مطالعه مطالب علمی بیشتر به صفحه مقالات آموزشی سایت باشگاه نانو مراجعه نمایید.

۴-مراجع

[1]. Allen, Samuel M., and Edwin L. Thomas. The structure of materials. Vol. 44. New York: Wiley, 1999.

[2].Callister, William D., and David G. Rethwisch. Materials science and engineering: an introduction. Vol. 7. New York: John wiley& sons, 2007.

[3]. De Graef, Marc, and Michael E. McHenry. Structure of materials: an introduction to crystallography, diffraction and symmetry. Cambridge University Press, 2012.

۵- پاورقی‌ها

[1]Oblique

[2] Simple Cubic

[3] Body Centered Cubic

[4] Face Centered Cubic

[5]Packed Vector

[6] Atomic Packing Factor

[7]Hexagonal Closed Packed